How to Implement Graph Data Structure in Java

This Comprehensive Java Graph Tutorial Explains Graph Data Structure in detail. It includes how to Create, Implement, Represent & Traverse Graphs in Java:

A graph data structure mainly represents a network connecting various points. These points are termed as vertices and the links connecting these vertices are called 'Edges'. So a graph g is defined as a set of vertices V and edges E that connect these vertices.

Graphs are mostly used to represent various networks like computer networks, social networks, etc. They can also be used to represent various dependencies in software or architectures. These dependency graphs are very useful in analyzing the software and also at times debugging it.

Read More About Java Course in Pune

Java Graph Data Structure

Different Variants Of Graph

• Directed Graph
• Weighted Graph

How To Create A Graph?

Graph Representation In Java

• Adjacency Matrix
• Adjacency List

Java Graph Data Structure

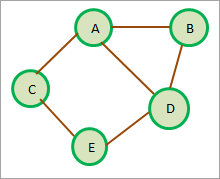
Given below is a graph having five vertices {A,B,C,D,E} and edges given by {{AB},{AC},{AD},{BD},{CE},{ED}}. As the edges do not show any directions, this graph is known as 'undirected graph'.

Apart from the undirected graph shown above, there are several variants of the graph in Java.

Let's discuss these variants in detail.

Different Variants Of Graph

The following are some of the variants of the graph.

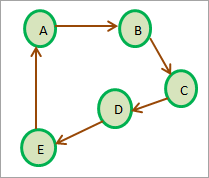
#1) Directed Graph

A directed graph or digraph is a graph data structure in which the edges have a specific direction. They originate from one vertex and culminate into another vertex.             

In the above diagram, there is an edge from vertex A to vertex B. But note that A to B is not the same as B to A like in an undirected graph unless there is an edge specified from B to A.

A directed graph is cyclic if there is at least one path that has its first and last vertex as the same. In the above diagram, a path A->B->C->D->E->A forms a directed cycle or cyclic graph.

Conversely, a directed acyclic graph is a graph in which there is no directed cycle i.e. there is no path that forms a cycle.

#2) Weighted Graph

In a weighted graph, a weight is associated with each edge of the graph. The weight normally indicates the distance between the two vertices. The following diagram shows the weighted graph. As no directions are shown this is the undirected graph.

Note that a weighted graph can be directed or undirected.

How To Create A Graph?

Java does not provide a full-fledged implementation of the graph data structure. However, we can represent the graph programmatically using Collections in Java. We can also implement a graph using dynamic arrays like vectors.

Usually, we implement graphs in Java using HashMap collection. HashMap elements are in the form of key-value pairs. We can represent the graph adjacency list in a HashMap.

A most common way to create a graph is by using one of the representations of graphs like adjacency matrix or adjacency list. We will discuss these representations next and then implement the graph in Java using the adjacency list for which we will use ArrayList.

Graph Representation In Java

Graph representation means the approach or technique using which graph data is stored in the computer's memory.

We have two main representations of graphs as shown below.

Adjacency Matrix

Adjacency Matrix is a linear representation of graphs. This matrix stores the mapping of vertices and edges of the graph. In the adjacency matrix, vertices of the graph represent rows and columns. This means if the graph has N vertices, then the adjacency matrix will have size NxN.

If V is a set of vertices of the graph then intersection Mij in the adjacency list = 1 means there is an edge existing between vertices i and j.

To better understand this concept clearly, let us prepare an adjacency Matrix for an undirected graph.

As seen from the above diagram, we see that for vertex A, the intersections AB and AE are set to 1 as there is an edge from A to B and A to E. Similarly intersection BA is set to 1, as this is an undirected graph and AB = BA. Similarly, we have set all the other intersections for which there is an edge to 1.

In case the graph is directed, the intersection Mij will be set to 1 only if there is a clear edge directed from Vi to Vj.

This is shown in the following illustration.

As we can see from the above diagram, there is an edge from A to B. So intersection AB is set to 1 but intersection BA is set to 0. This is because there is no edge directed from B to A.

Consider vertices E and D. We see that there are edges from E to D as well as D to E. Hence we have set both these intersections to 1 in the adjacency Matrix.

Now we move on to weighted graphs. As we know from the weighted graph, an integer also known as weight is associated with each edge. We represent this weight in the adjacency Matrix for the edge that exists. This weight is specified whenever there is an edge from one vertex to another instead of '1'.

This representation is shown below.

Adjacency List

Instead of representing a graph as an adjacency matrix which is sequential in nature, we can also use linked representation. This linked representation is known as the adjacency list. An adjacency list is nothing but a linked list and each node in the list represents a vertex.

The presence of an edge between two vertices is denoted by a pointer from the first vertex to the second. This adjacency list is maintained for each vertex in the graph.

When we have traversed all the adjacent nodes for a particular node, we store NULL in the next pointer field of the last node of the adjacency list.

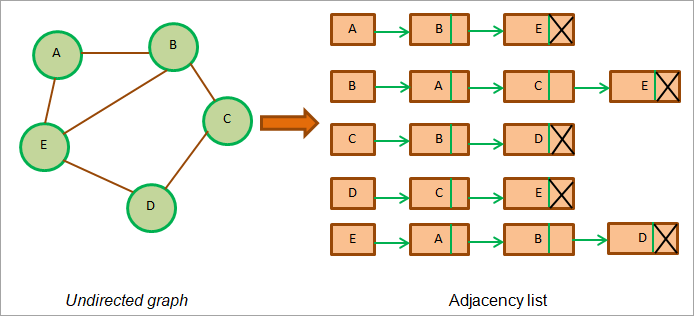
Now we will use the above graphs that we used to represent the adjacency matrix to demonstrate the adjacency list.

The above figure shows the adjacency list for the undirected graph. We see that each vertex or node has its adjacency list.

In the case of the undirected graph, the total lengths of adjacency lists are usually twice the number of edges. In the above graph, the total number of edges is 6 and the total or sum of the length of all the adjacency lists is 12.

Now let's prepare an adjacency list for the directed graph.

As seen from the above figure, in the directed graph the total length of the adjacency lists of the graph is equal to the number of edges in the graph. In the above graph, there are 9 edges and sum of the lengths of adjacency lists for this graph = 9.

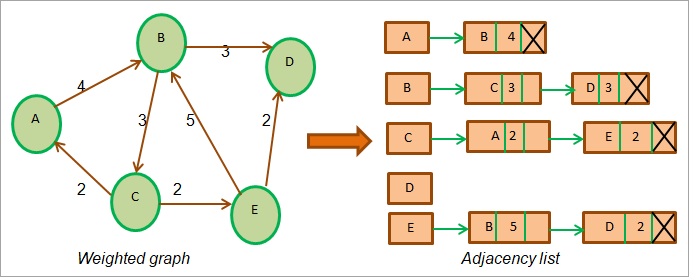
Now let us consider the following weighted directed graph. Note that each edge of the weighted graph has a weight associated with it. So when we represent this graph with the adjacency list, we have to add a new field to each list node that will denote the weight of the edge.

The adjacency list for the weighted graph is shown below.

The above diagram shows the weighted graph and its adjacency list. Note that there is a new space in the adjacency list that denotes the weight of each node.

Prepare For your Java Career:

Want to learn more about Java? SevenMentor will show you how to showcase them on your resume. And don’t forget about your hard skills. While soft skills are important, your technical skills are what you’ll use to get the job done. Check out our Java classes in Pune to start building your technical skills. Whether you want to become a Java developer, we’ll guide you along every step of the way. We’ll even help you prepare for interviews, with code challenges, tips from recruiters, and other helpful resources you can find in our career center. 

Original Source: https://kiranvermablog.wordpress.com/2022/06/18/java-graph-tutorial-how-to-implement-graph-data-structure